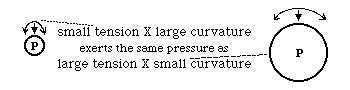
More on D'Arcy Thompson and tensor variables Pressure difference equals Curvature multiplied times Tension. dP = C x T dP = T/R        where R is the radius of curvature Because both curvature and tension often vary with direction dP = C x T + c x t      c and t are curvature and tension in the axis perpendicular to C and T dP = T/R + t/r      R and r are radii of curvature in two perpendicular directions Unfortunately, D'Arcy Thompson and many others mistakenly used this equation dP = T x (1/R + 1/r)      Which assumes that tension is the same in all directions. For soap bubbles, tension really is the same in all directions. But for cell sheets and surfaces of living, actively contractile cells, tension usually varies as some function of direction, therefore the correct equations are dP = C x T + c x t = T/R + t/r This and other simple mistakes have led biophysics down a blind alley.   Complete copy of D'Arcy Thompson's book, On Growth and Form The same book as a text file (no illustrations but easier to search for key words or topics) How to think about quantitative variables that vary with direction? (like curvature, tension, permeability, strain, and others). Variables that don't have any directionality are called scalars. Chemical concentrations, density, temperature, osmotic pressure, & hydrostatic pressure are scalars. Scalars have an amount at each location, which can differ with location; but has no direction. Vectors have an amount and a direction at each location. Electric fields are an example of a vector variable. Curvature, tension (equals "stress", which includes tensile stress and compressive stress) and "strain" and permeability are all examples of variables that can and often do have different amounts in different directions. Variables that differ with direction are called tensors, and unfortunately are not included in the education of anybody but mathematicians and some engineers. In my opinion, tensors are more important for embryology than vectors. All you need to know about tensors are the following: 1) Curvature, stress (tension) and strain (% distortion produced by stress) are second order symmetrical tensors. 2) (most) Vectors are considered to be first order tensors. Scalars are zeroeth order tensors. 3) Elastic moduli are fourth order symmetrical tensors. That means their variation with direction can be more complicated than if they were second or third order tensors. 4) The word "Symmetric" applied to tensors means that for every two opposite directions, their value is the same. [Don't worry about it, but axial vectors are really second order anti-symmetric tensors.] 5) For second order tensors, if they vary with direction (which they CAN, but don't have to), their minimum and maximum directions are always exactly perpendicular to each other. D'Arcy Thompson's biggest mistake was to treat mechanical tension as if it could not vary with direction, which greatly narrowed and reduced how many geometric shapes he could "explain". He could only recognize the possibility of direct causation by forces when objects had shapes that could be produced by tensions that were equal in all directions and at all locations. (spheres, catenoids, etc. the sums of whose curvatures are constant everywhere, as in soap bubbles). It is a tragedy that so many people have such strong positive or negative responses to D'Arcy Thompson, but nobody analyzes his tacit assumptions, nor why these assumptions are misguided. Incidentally, tensors played a major role in the escape of physics from the "ether" concept, which was analogous to "positional information" in today's embryology. D'Arcy Thompson mistakenly persuaded himself and his readers that self-building shapes can only result from tensions that don't vary with direction. Malcolm Steinberg (and Scott Gilbert) became persuaded that convergence to any consistent geometry, via two or more alternative sequences of intermediate geometries, can only be caused by forces that are reversible, conservative and minimize free energy. Mathematicians tend to think that they somehow "own" the concept of tensors, think of them more in the sense of "transformation of number matrices", not as physical variables.