Do you understandwhy the weather is so much harder to predict than the tides?

Most people assume that erratic or complex patterns of behavior in a system mean that this system must be governed by complex equations and/or by many different external factors. Conversely, most people also assume that simple behavior indicates that a system is goverened by simple equations and few inputs. Thus, if a system switches from simple predictable behavior to irratic and unpredictable behavior, almost everyone this means that a new and very different set of equations have taken over governing it. Plausible; but WRONG!
The following simple "difference equation" is relevant to many biological situations, including any autocatalytic syntheses and especially the famous "logistic equation" governing population growths:

X_{(next time)} = a * X_{(this time)} * (1 - X_{(this time)})

You start out with any value of X between zero and one; and set the parameter "a" to be any number from zero to four. The Macintosh computer program named "Parabola_Feigenbaum" will show you the behavior of the system for increasing values of the parameter "a" (starting at 2.00) and using random initial values of X.

We used to be able to run these programs directly on your computer, by clicking on their names. We need someone to translate them into Java, so that students will be able to run these programs again.

X_{(next time)} = a * X_{(this time)} * (1 - X_{(this time)})

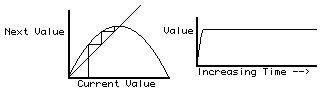
The results are plotted both on the lower right (time on the horizontal axis, and X on the vertical axis) and superimposed on a graph of the curve for this equation (an upside-down parabola). Next, these results are erased, the value of "a" is increased by 0.01 (one one-hundredth) and the whole process is repeated. The point is that X homes in on a certain value; that value is plotted (cumulatively, i.e. not erased) as a function of "a" in the upper-right area of the computer screen ("a" on the horizontal axis, X on the vertical axis).

Things to watch for: Does X always home in on the same value? Or does this preferred value change slowly as a function of "a"? What happens when the value of "a" reaches about 3? Are there any changes in how long it takes the value of X to home in? Or in whether it over-shoots? When does it start jumping back and forth between two values? Do these two values change in any consistent way? What happens when a is even bigger? Notice little "windows" in higher values of "a" in which the system reverts back to homing in on just one or a few values of X? Do parts of the plot (in the upper right) of X versus "a" look at all like miniature versions of the whole plot (incidentally, this plot is a fractal and has the property of "self-similarity": in the sense that parts are miniatures of the whole. (it is a simpler relative of infamous Mandelbrot set).

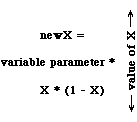
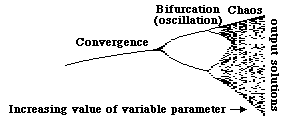
Notice how small quantitative changes in the parameter "a" controls how X behaves. Low values of "a" cause X to home in toward a single value (an example of what is called asymptotic stability and an attractor basin, two concepts that will be more fully discussed in a later section); higher values of "a" instead cause X to oscillate spontaneously (in a limit cycle); and still larger values of "a" create a "strange attractor", the special property of which is to cause what seems like random jumping around between many, many different values, perhaps even an infinite number of seemingly random values. Such behavior seems totally irregular, accidental and unpredictable; but it is actually just as determinate as the simple oscillations. Such behavior has come to be called "chaos", although a better term might have been "pseudo-chaos", or deterministic chaos: the behavior only seems random, indeterminate, without underlying order. It had long been assumed that chaotic behavior must mean that a system is either under the control of unknowably many different factors, or that there is no true causation involved. The best-selling book "Chaos" describes how several applied mathematicians, using computers experimentally to study various positive feed-back equations derived from studies of weather, turbulence and ecological cycles, found out that equations don't have to be complex or indeterminate to generate what seems to be chaotic behavior.

A key concept here is that of "sensitive dependence on initial conditions": if you start out with exactly the same combination of initial values, then the system's subsequent behavior will, of course, likewise be exactly the same. Thus, the question is, what happens if the initial conditions are made only slightly different: will the system's behavior then also differ only slightly (or perhaps not at all, in the case of asymptotic stability, where the results would converge toward being identical); or will two systems with slightly different beginning points therefore diverge progressively more and more, to such an extent that the results eventually become qualitatively different? The latter is what happens in the case of a strange attractor, and the result is "chaos". Many people have come to believe that the difficulty of predicting the weather (among other things) is neither because the weather depends on so many different variables, nor because it depends on especially complicated equations, but rather because those equations that it does depend on happen to have the properties of a strange attractor.

From the point of view of an embryologist, an interesting question is whether the progressive changes in the different parts of a developing embryo, and particularly the spontaneousness of these changes, with tiny initial differences in different parts of the egg spontaneously magnifying themselves into big differences, and then the results somehow homing in on certain geometric patterns, may not have to be explained in terms of the governing equations somehow crossing over into something like the zone of the strange attractors (in order to generate patterns), and then retreating back into the zone of simple attractor basins (in order to stabilize the resulting patterns).

One question raised by such discoveries is how (or whether!) one can tell the difference between fluctuations which only seem to be random, unpredictable and indeterminate (but are really the result of a strange attractor), as opposed to those whose causation really is as complicated as people used to assume. For example, Prof. Salmon and his recent PhD student Bob Skibbens accumulated a lot of data on the back and forth movements of chromosomes lined up along the metaphase plate in mitosis. These oscillations looked rather chaotic, but is this deterministic pseudo-chaos like that produced by the equations above; or is it real old-fashioned chaos in the sense of being caused by numerous, random, unknowably complicated variables? To answer this question, you would need to accumulate enough data for fractal-like properties of self-similarity to start to appear (analogous to the right-hand side of the most recent figure above). This turns out to be the litmus test: whether the seemingly chaotic pattern contains a fractal, the key property being self-similarity, which means that a magnified view of the pattern looks like the original pattern itself, if you can imagine a pattern made out of lots of miniature scale models of itself, with each of the scale models itself being made out of tinier scale models, more or less forever. Another interesting property of fractal patterns is that they are considered to have non-integer dimensions - imagine something which is neither 2-dimensional nor 3-dimensional, but that instead has a dimension of 2.4356, or something like that!

But it's not quite clear to me what you would gain by knowing that? They already knew that the chromosomes' positions tended to gravitate toward the metaphase plate; so clearly there is some kind of negative feedback. Is the equation for this negative feedback very complicated with random inputs (thus producing old-fashioned non-deterministic chaos); or does this negative feedback obey a simple equation, but with the equivalent of its "a" parameter set to a high enough value that the net behavior seems random. Wouldn't you rather just know what the equation is, and what the molecular mechanisms of the feedback are?

A question for class discussion: Suppose that treating these cells with a small amount of a certain chemical caused the oscillations of chromosome position to become more regular, with a constant frequency: What would you tentatively conclude from this? Continuing this line of reasoning, what might be the effect of adding a bit more of this drug? Likewise, can you think of some biological phenomena which normally either oscillate at steady rates, or gravitate to some set value; in these cases, suppose that it were possible to increase something alalogous to the parameter "a". What might happen? Consider the case of heart beating: Do you know what is meant by fibrillation (when the heart beats chaotically, killing you)?

When I read the book "Chaos", I wondered whether the unexpected chaotic behavior of the equation X(next time) = a * X(this time) * (1 - X(this time)) might be some special property of the particular equation used. So I wrote a variant program in which you use the mouse to enter any shaped curve that you want; the program then uses this curve in place of the upside-down parabola as the basis for its repeated recalculation of X, with corresponding 1/100th magnifications of the height of the curve (corresponding to the increases in the variable parameter "a". This program was also available; it was called Feigenbaum_DrawEquation. You could draw whatever shaped curve you like in the space provided (pushing the mouse button initiated the drawing sequence, while this sequence was automatically concluded once you moved the mouse-arrow far enough toward the right-hand edge of the screen).

* Can you discover what properties in the curve lead to which peculiarities in the plot of preferred X values as a function of vertical magnification?

* If someone showed you just the plot of X versus "a", to what extent could you deduce the approximate shape of the original curve of X(next time) versus X(this time)?

The property of self-similarity is also possessed by many biological structures. For example, the branching patterns of trees, lungs and possibly even some nerve cells can be quite self-similar, in the sense that if you compare the whole pattern with a magnified view of part of the structure, it will seem to have much the same geometrical pattern. What are the causes of this self-similarity? Books on fractals and chaos tend to create the impression that this cause may be analogous to the cause of self-similarity in patterns created by chaotic phenomena, such as in the Feigenbaum tree pattern produced by the simple feed-back equation discussed above. A favorite example is the "Barnesly fern" pattern generated by repeated applications of a another simple equation. These patterns really do look very much like ferns.

Mandelbrot Sets are easier to understand and generate than you may think:

Some people seem to prefer being mysitified by this subject; anyway the television programs and picture books seldom give you enough information to understand how they are made or what they mean; but actually the principles are not difficult.

The first step in understanding how the Mandelbrot set is generated is to visualize an ordinary sheet of graph paper being used to represent complex numbers as points on the graph paper plane; you remember complex numbers? Those are the ones like "minus two plus one times the square root of minus one". That particular complex number is represented by the point two unit distances to the left of the vertical axis, and one unit distance upward from the horizontal axis, as shown in the computer-generated figure below.

The second step is to imagine the computer being assigned to take each little tiny point on this plane, one at a time, and carrying out the following (rather arbitrary!) calculation: square the complex number and add the result to the original number. Then you take whatever new complex number number is produced by that operation, and square IT, and then add the original complex number to that square. And then take that answer, and square IT, and add the result to the original number. And do it again and again and again.

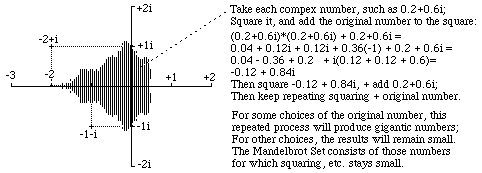
The following are an actual series of results of this operation: "Square and add back the original number"

        0.2        + 0.6i
       -0.12       + 0.84i
       -0.4912     + 0.3984i
        0.2825     + 0.2086i
        0.2363     + 0.7179i
       -0.2595     + 0.9393i
       -0.6149     + 0.1125i
        0.5655     + 0.4617i
        0.3066     + 1.1222i
       -0.9652     + 1.2883i
       -0.5278     - 1.8867i

The third step is to color each part of the graph paper differently according to how many steps it takes for the repeated "square and add original number" operation to produce a number bigger than, say, +/- 1000. The tradition is if a given initial number never does produce big numbers, then color that part of the plane black. The region of initial complex numbers for which repeated squaring, etc. keeps giving small numbers is the set of numbers that Mandelbrot modestly named after himself: The Mandelbrot Set. (But then, what are you going to do if your name means "almond bread" in German?)

Julia Sets, and why they resemble local parts of the Mandelbrot Set:

At higher resolution, it becomes apparent that each Julia Set closely resembles the part of the Mandelbrot set located near the particular complex number you added back to the squares. This may seem slightly magical at first; but when you think carefully about it, it makes perfect sense. After all, in each part of the Mandelbrot set, the number you are adding to the squares is the number that corresponds to that particular area. Thus, no wonder than each Julia Set looks like some sort of magnified "variations on a theme" of the part of the Mandelbrot Set that corresponds to the constant number.

The key property of these and other fractals is that if you magnify little bits of them you see what amount to lots of little "scale models" of the original pattern; and if you magnify them further, you see that the parts of the parts also have the shape of even tinier scale models of the original; and that goes on forever. You might wonder what one means by "magnifying" part of the pattern: it simply means modifying your computer program so that it does its calculations starting with numbers that are closer together in the first place: so instead of trying the squaring etc with -2 + 2i, and then -1.99 + 2i, and then -1.98 + 2i etc., instead your second initial number would be (say) -1.99999 + 2i, and your next intial number would be -1.99998 + 2i, etc. That would give you a thousand-fold increase in resolution and magnification.

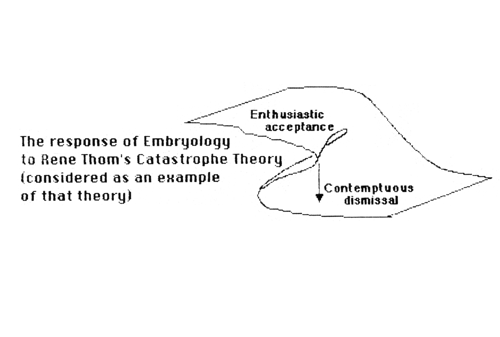
Catastrophe Theory

Some basic underlying concepts of Catastrophe Theory: (worth knowing in their own right)

Stability: anything that resists change has some kind of stability.

Asymptotic Stability is possessed by systems which somehow gravitate to some preferred state: like a ball rolling down to the lowest point in a cup, or a weighted punching dummy rotating back to a vertical position after you punch it, or the restoration of any homeostatic physiological property like body temperature. The minimization of free energy by thermodynamically closed ,"Hamiltonian" , systems is a special kind of asymptotic stability; the only one encountered in most scientists' educations, but not the only kind that exists!
Homeostasis: Animal (and plants) have many physiological mechanisms that serve to resist change and keep all sorts of properties (body temperature, blood pH, salt concentrations, etc.) approximately constant. Their basic principle of operation is variation of relative strengths of opposing pairs of mechanisms, with these strengths varying as functions of the variables (like temperature) that are being controlled, and balancing at the desired values.

Attractor Basin: There are usually only a limited range of values of the stable variables from which the system is able to gravitate back to its preferred state; this is analogous to the limits of a valley; beyond the ridge line of which the system will instead gravitate into other basins. Death is when you get outside the homeostatic basins!

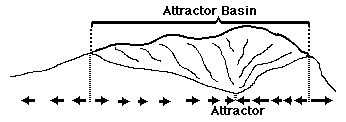
Structural Stability: (Does not refer specifically to physical structures!)
When the asymptotic stability of a system is retained even if one changes some of the underlying controlling variables (e.g. moves some of the weights in the punching dummy), then the state of stability itself has a kind of higher-order stability. The word "structural" is being used here in the sense of inherent, built-in, or innate. The system remains qualitatively the same (the punching dummy still rotates back, etc.) despite internal changes.

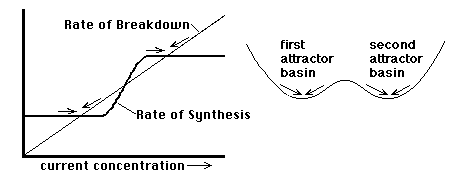
Catastrophe Set: As a rule, however, if you change the control variables too much, then eventually the attractor basin of the old asymptotic stability will be destroyed. This means that the system will jump spontaneously to some new state. The jump is called the catastrophe and the particular combinations of values of control variables along the boundary where you have finally broken the camel's back are called the catastrophe set ("set" in the mathematical sense of a collection). In the case of the punching dummy analogy, if you move the lead weight far enough, then eventually the dummy will roll spontaneously so that its side, or maybe its head, is down. When disturbed, it now gravitates to this new state.

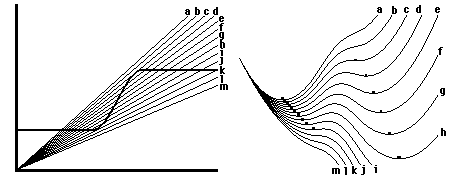
From this perspective, it is worth considering that developing embryos do tend to jump successively from one morphological state to the next, with each state being able to resist disturbance and even repair damage, but eventually undergoing spontaneous (and mysterious) rearrangements of parts.

• * In what respects does this correspond to the predictions of catastrophe theory?
  * If it does, how does this help us to make sense of developmental mechanisms?

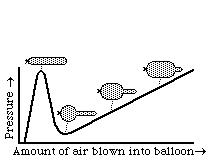
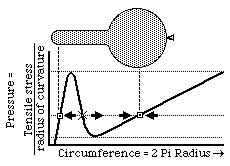
When you inflate a balloon, why do you have to blow hardest right at first? How can one end of a long balloon seem to have a higher internal pressure than the other? [HINT: Both questions have the same answer.]

Some general ideas from Rene Thom's book "Structural Stability and Morphogenesis"

Qualitative versus Quantitative: Despite disparaging quotes from physicists such as Kelvin and Rutherford ("Qualitative is only poor quantitative."), developments in higher mathematics over the past century have been away from the quantitative and toward the qualitative. The work of the turn-of-the-century French mathematician Poincaré was particularly important in this repect.
Ask yourself: is it more important to know the exact speed of the earth through space (quantitative information), or to know (qualitative information) whether or not it will spiral into the sun in the next few years?

Suppose that the graph below on the left represented actual data, and you were trying to choose between several explanatory hypotheses of a mathematical nature.

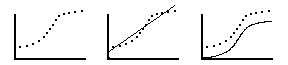
   data to be explained      hypothesis #1            hypothesis #2

If theory A predicts a straight line proportionality (middle graph), while theory B predicts the sigmoidal curve on the right, then which hypothesis seems to be more likely to be on the right track, in a qualitative sense, even though the predicted curve touches none of the data points?

Many physical phenomena turn out to depend on the qualitative properties of the laws/equations that control/describe them in the sense that the same basic events will occur over a wide range of (say) y-intercepts of a curve, or even with a wide range of different slopes of that curve, so long as it is convex upward, or other things like that. One example is that the odd behavior of balloons (the questions at the bottom of the previous page) depends on the non-linear proportionality between tension and amount of stretching of rubber. If the tension of a material increased in exact proportion to how much it was stretched, then a balloon made out of that material wouldn't have these behaviors. Another example is that when you oil a hinge to keep it from squeaking, part of what you accomplish is a quantitative reduction in friction, but the actual elimination of the noise results from reducing the previous non-linearity of the proportionality between frictional resistance and speed of displacement (that had led to "stick-and-slip" vibrations).

Rene Thom's ideas concerning the "repeatability" of experiments:

All experimental science is based on the expectation that experiments will be repeatable
To say that an experimental result is "not repeatable" is to suggest that the result is not true ćat least a mistake, and perhaps even a fraud. It is one of the worst things that anyone can say about your work! Obviously, however, repeatability depends on whether you can duplicate the initial and surrounding pre-conditions precisely enough. If the pre-conditions aren't the same, then it isn't fair to expect the results to be the same; they may or may not be, depending on whether the differences "matter".
But such preconditions can never be reproduced with utter exactness; there will always be some small differences. This brings us to Thom's essential point, which is that there can be wide differences in the degree of sensitivity to these (inevitable) differences in pre-conditions: some physical situations, and some combinations of equations, happen to be highly susceptible to very small initial differences. Thom argues that scientists have historically shyed away from all those phenomena that have too great a degree of sensitivity to initial conditions. In other words, scientists have historically confined their interests mostly to phenomena that happen to have the property of structural stability (so that where sufficiently small quantitative changes in conditions do not result in major qualitative changes in end results). Conversely, they have systematically averted their gaze from the catastrophe sets. This, he suggests, rather than any inherent complexity or other difficulty, is why scientific progress has lagged so much in regard to such topics as turbulence, weather, pattern-generating systems, mathematical aspects of biology, psychology and other topics.